import QuantLib as ql
from matplotlib import pyplot as pltDangerous day-count conventions
This notebook (based on a question by Min Gao on the QuantLib mailing list. Thanks!) shows one possible pitfall in the instantiation of term structures.
today = ql.Date(22, 1, 2018)
ql.Settings.instance().evaluationDate = todayThe problem
Talking about term structures in Implementing QuantLib, I mention that they need to be passed a day-count convention and I suggest to use simple ones such as Actual/360 or Actual/365. That’s because the convention is used internally to convert dates into times, and we want the conversion to be as regular as possible. For instance, we’d like distances between dates to be additive: given three dates \(d_1\), \(d_2\) and \(d_3\), we would expect that \(T(d_1,d_2) + T(d_2,d_3) = T(d_1,d_3)\), where \(T\) denotes the time between dates.
Unfortunately, that’s not always the case for all day counters. The property holds for most dates…
dc = ql.Thirty360(ql.Thirty360.USA)
T = dc.yearFractiond1 = ql.Date(1, ql.January, 2018)
d2 = ql.Date(15, ql.January, 2018)
d3 = ql.Date(31, ql.January, 2018)print(T(d1, d2) + T(d2, d3))
print(T(d1, d3))0.08333333333333334
0.08333333333333333…but doesn’t for some.
d1 = ql.Date(1, ql.January, 2018)
d2 = ql.Date(30, ql.January, 2018)
d3 = ql.Date(31, ql.January, 2018)print(T(d1, d2) + T(d2, d3))
print(T(d1, d3))0.08055555555555556
0.08333333333333333That’s because some day-count conventions were designed to calculate the duration of a coupon, not the distance between any two given dates. They have particular formulas and exceptions that make coupons more regular; but those exceptions also cause some pairs of dates to have strange properties. For instance, there might be no distance at all between some particular distinct dates:
d1 = ql.Date(30, ql.January, 2018)
d2 = ql.Date(31, ql.January, 2018)
print(T(d1, d2))0.0The 30/360 convention is not the worst offender, either. Min Gao’s question came from using for the term structure the same convention used for the bond being priced, that is, ISMA actual/actual. In fact, it seemed like a natural thing to do. However, this convention needs to be given a reference period for its calculations, as well as the two dates whose distance one needs to measure; failing to do so will result in the wrong results…
d1 = ql.Date(1, ql.January, 2018)
d2 = ql.Date(15, ql.January, 2018)
reference_period = (
ql.Date(1, ql.January, 2018),
ql.Date(1, ql.July, 2018),
)dc = ql.ActualActual(ql.ActualActual.ISMA)
print(dc.yearFraction(d1, d2, *reference_period))
print(dc.yearFraction(d1, d2))0.03867403314917127
0.038356164383561646…and sometimes, in spectacularly wrong results. Here is what happens if we plot the year fraction since January 1st, 2018 as a function of the date over that same year.
d1 = ql.Date(1, ql.January, 2018)
dates = [(d1 + i) for i in range(366)]
times = [dc.yearFraction(d1, d) for d in dates]ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.plot([d.to_date() for d in dates], times, "-");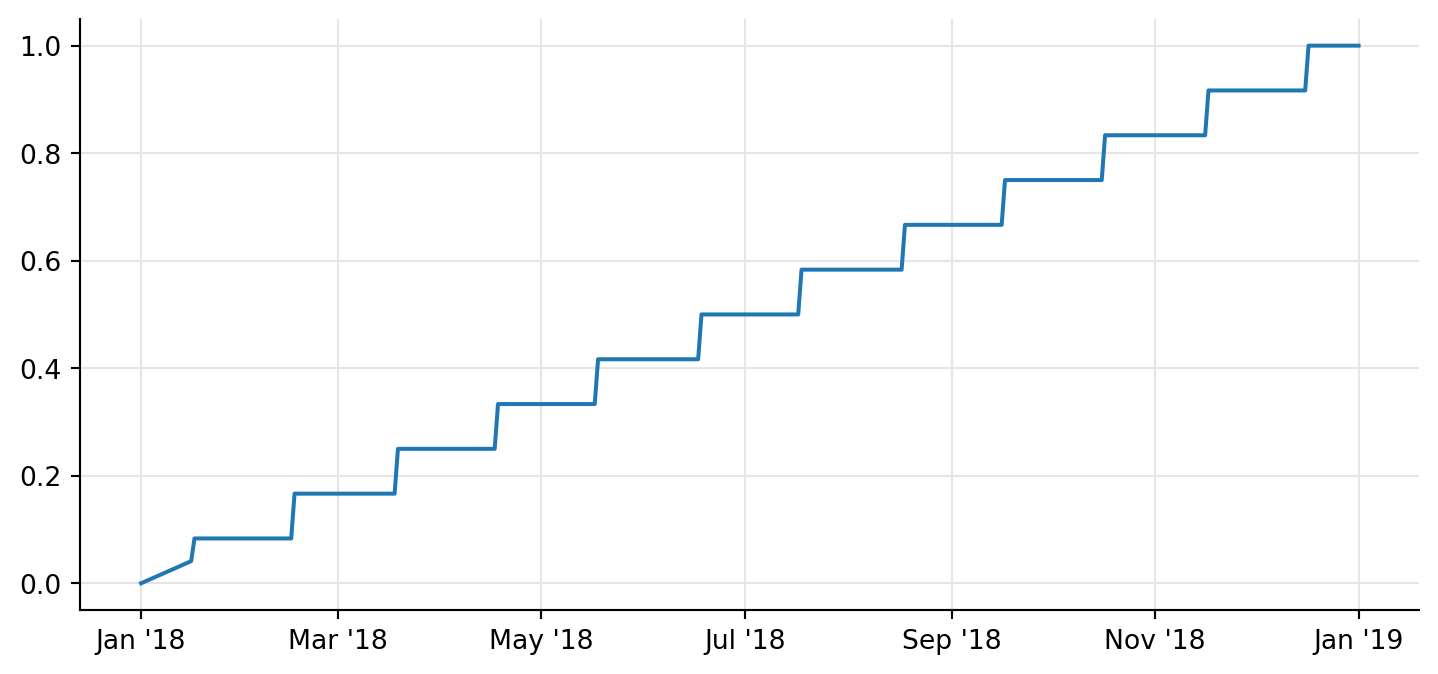
Of course, that’s no way to convert dates into times. Using this day-count convention inside a coupon is ok, of course. Using it inside a term structure, which doesn’t have any concept of a reference period, leads to very strange behaviors.
curve = ql.FlatForward(today, 0.01, ql.ActualActual(ql.ActualActual.ISMA))dates = [(today + i) for i in range(366)]
discounts = [curve.discount(d) for d in dates]
ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.plot([d.to_date() for d in dates], discounts, "-");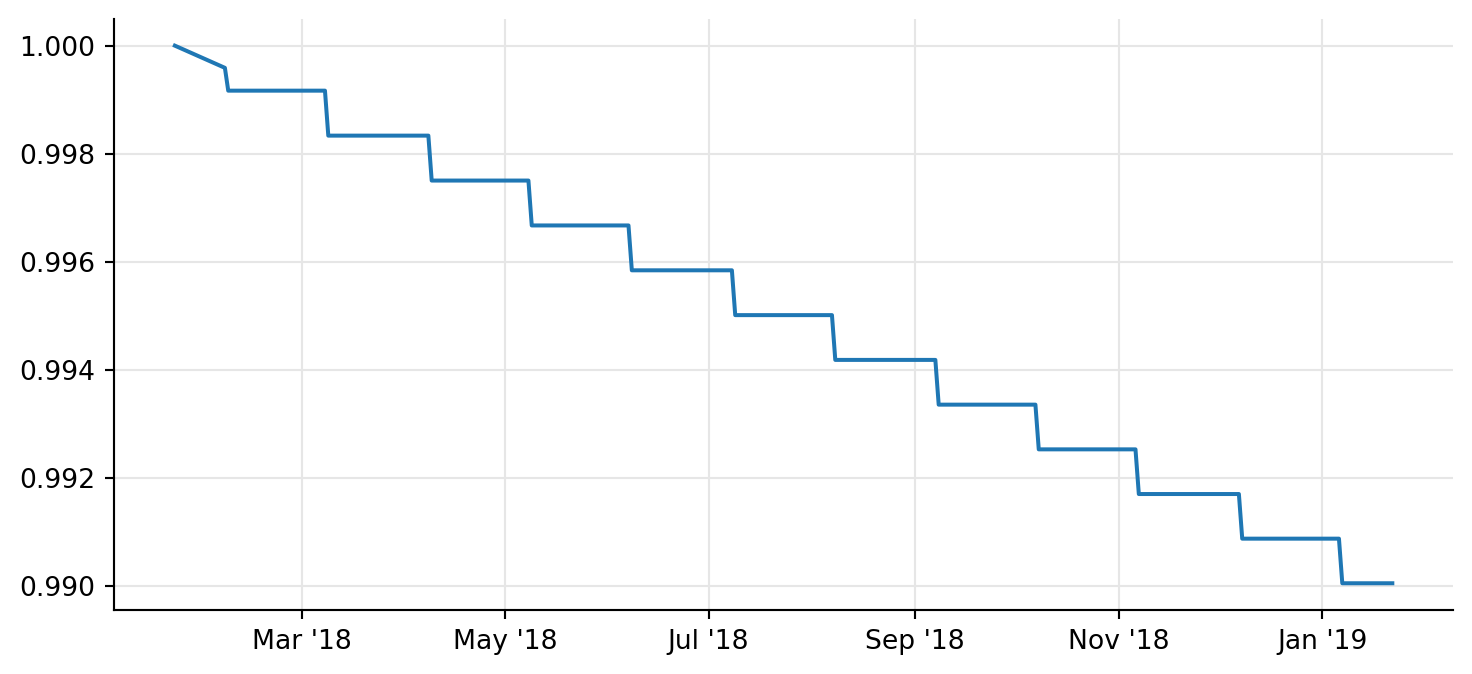
Why did we allow to use this convention without passing the reference period? Well, we couldn’t make it non optional in the call to yearFraction, because that would have made its interface different from what is declared in the base DayCounter class. Making it non-optional in the base-class method would have been inconvenient for all other convention that don’t need it. At the time, we probably didn’t think (memories of the early times of the library are quickly fading) of keeping the common interface and raising an error for this convention if the reference dates weren’t passed. I’m not sure we can safely make that change now.
Any solutions?
Not really, at least not in a general way. For a specific bond, it is possible to store a schedule inside an ISMA actual/actual day counter and use it to retrieve the correct reference period for dates within a coupon:
schedule = ql.MakeSchedule(
effectiveDate=ql.Date(1, ql.January, 2018),
terminationDate=ql.Date(1, ql.January, 2025),
frequency=ql.Annual,
)
dc = ql.ActualActual(ql.ActualActual.ISMA, schedule)This way, the calculations seem to be consistent…
d1 = ql.Date(1, ql.January, 2018)
d2 = ql.Date(15, ql.January, 2018)
reference_period = (
ql.Date(1, ql.January, 2018),
ql.Date(1, ql.July, 2018),
)
print(dc.yearFraction(d1, d2, *reference_period))
print(dc.yearFraction(d1, d2))0.038356164383561646
0.038356164383561646…and conversion from dates to times seems to be reasonable.
d1 = ql.Date(1, ql.January, 2018)
dates = [(d1 + i) for i in range(366)]
times = [dc.yearFraction(d1, d) for d in dates]
ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.plot([d.to_date() for d in dates], times, "-");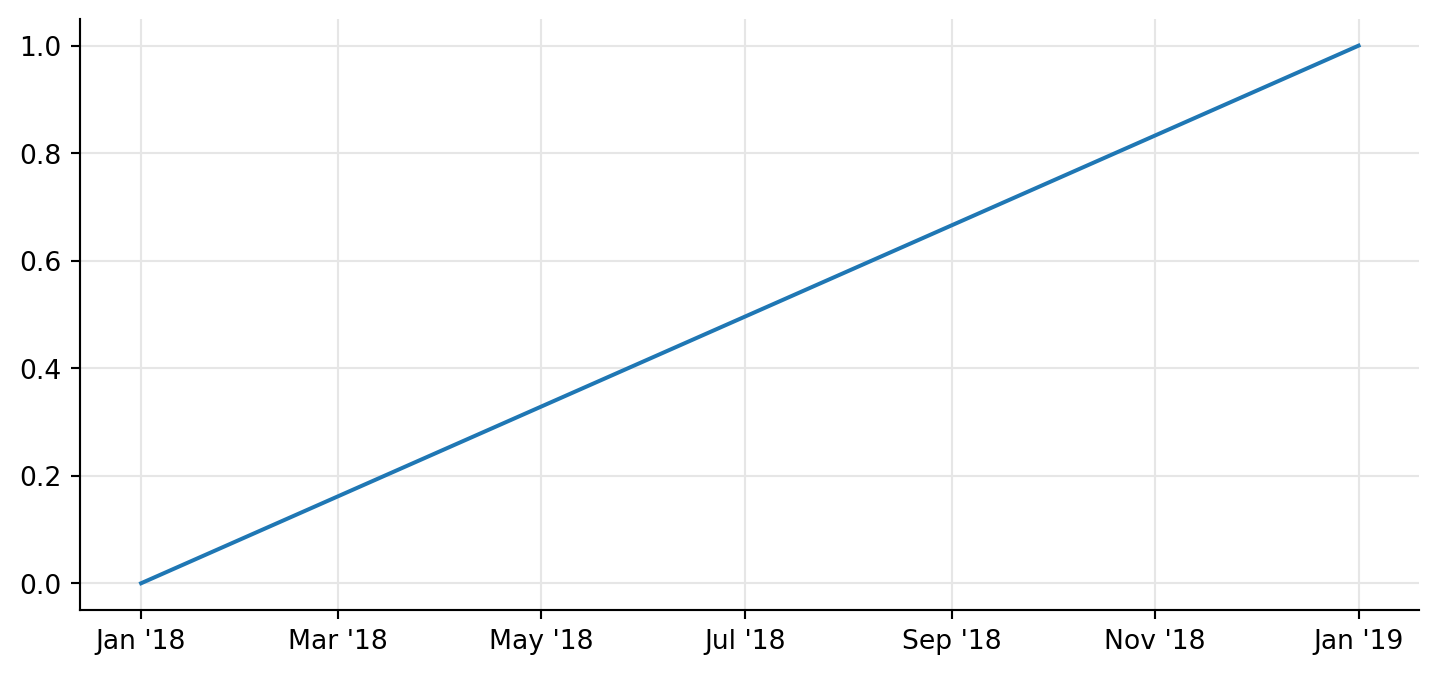
However, that’s probably not the best choice for a curve. The calculation is bound to a specific bond, which is not great if you want to use the curve as a generic one for multiple instruments. Also, the calculation only works within the range of the schedule, and will give you an error if you try to go outside them:
try:
dc.yearFraction(d1, schedule[-1] + ql.Period(10, ql.Days))
except Exception as e:
print(f"Error: {e}")Error: Dates out of range of schedule: date 1: January 1st, 2018, date 2: January 11th, 2025, first date: January 1st, 2018, last date: January 1st, 2025Therefore, I stand by my suggestion. When creating a bond, of course, you must use its specified day-count convention; but, unless something prevents it, use a simple day-count convention such as actual/360 or actual/365 for term structures. You can use a day-count convention bound to a particular schedule in some specific cases; for instance, calculating the yield of a specific bond.
